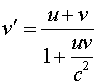 . Both u and v are
0.9c.
. Both u and v are
0.9c.Examples for relativity
Example #1
Problem:
A muon has a lifetime of 2.2E-8 s in its own rest frame. If it travels with a speed of 0.95c, how far will it travel before it decays?
Solution:
The distance if vt, but the time is longer by a factor g.
20.1 m
Example #2
Problem:
A meter stick flies by with an apparent length of 60 cm. What is its velocity?
Solution:
Starting with g equal to (1/0.6), solve for v.
v = 0.8c = 2.4E8 m/s
Example #3
Problem:
How much is the diameter of the Earth reduced due to the motion of the Earth around the sun.
DATA: Rearth_orbit=1.5E10 m, Dearth=1.28E7 m
Solution:
Calculate the Earth's velocity, using the circumference of the orbit and the length of a year in seconds. Then calculate the g factor. The earth is shorter by an amount D(1-1/g).
v = 2990 m/s, g = 1.0000000000497, Dx = 0.64 mm
Example #4
Problem:
Two space ships approach each other with velocities of 0.9c. According to an observer on the space ship, what is the velocity of the other ship.
Solution:
Use the velocity addition formula, 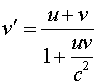 . Both u and v are
0.9c.
. Both u and v are
0.9c.
v' = 0.9944c
Example #5
Problem:
a.) Two space ships travel in the same direction, with one travelling at 0.9c, the other travelling at 0.99c. What is the velocity of the faster ship according to an observer on the slower ship.
Solution:
Again use the velocity addition formula, with u = 0.99c and v = - 0.9c.
v' = 0.825c
b.) What is the velocity of the slower ship according to an observer on the faster ship?
v' = -0.825c
Example #6
Problem:
A proton and an antiproton approach each other moving with a velocity of 0.999c. They fuse to form a new particle. What is the mass of the created particle?
Solution:
The energy of each proton is mp g c2 with the mass of the proton being 1.67E-27 kg. Multiplying it by two and dividing by c2 gives the new particle's mass.
m = 7.5E-26 kg