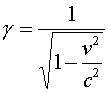
Momentum and energy
Perhaps the most famous equation in physics is
E = m c2 .
It expresses the fact that an object at rest has a large amount of energy as a result of its mass m . This energy is significant in situations where the mass changes, for example in nuclear physics interactions where nuclei are created or destroyed.
The energy of a moving object is of course still larger -- in Newtonian physics by an amount given by the well-known kinetic energy formula (1/2) m v2. The correct expression according to relativity is
E = g m c2
for the total energy, and henceE = (g - 1) m c2
for the kinetic energy, where g is the same relativity factor used previously:
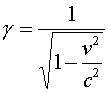
The momentum, which in Newtonian physics is given by m v, is given by
p = g m v
according to relativity.If the velocity v is small compared to c, the relativity formulas for momentum and kinetic energy become equivalent to their Newtonian (nonrelativistic) counterparts.
If the velocity v approaches c, both the momentum and energy approach infinity. Thus the velocity of an object that has any mass at all must always be less than c. However, there is no limit in principle to how large an object's momentum or energy can be.
The energy and momentum formulas can also be used to understand the case of particles like the photon that have zero mass. For the energy and momentum to remain finite in the limit m --> 0, it must be that g --> infinity, and hence v --> c. Thus particles with zero mass always travel with velocity c. The energy and momentum formulas imply p/E = v/c2, and hence p = E/c for zero-mass particles.