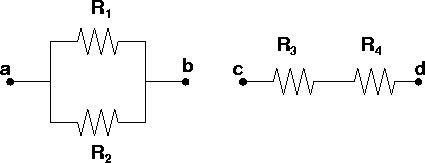
Resistors in series and parallel
Just as with capacitors, resistors can be lined up in series or parallel. Before we launch into a derivation, let us think about our expectations. We know that the resistance of a wire is proportional to length divided by the cross sectional area. Thus if we put resistors in series, end-to-end, we expect the resistances to add. If we put them in parallel, we expect the net resistance to be lowered. Consider the parallel and series cases below.

For the parallel case, we need to calculate the total current through the ab segment as a function of the voltage Vab.
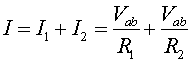
The resistance is the ratio of the applied voltage to the current.
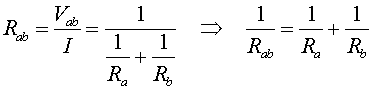
For resistors in series the effective resistance is simply the sum of the resistances.
![]()
Thus we have found that
Note that the rules for adding series or parallel resistors are opposite to the rules for adding capacitors.