


Next: Fortran Implementation
Up: Truncated Power Series
Previous: Truncated Power Series
In this worksheet, you will write a Fortran program that will evaluate the
error function of a real or complex number. You will use
 to check your answers, because it has this function built in.
to check your answers, because it has this function built in.
For small argument x, a good and efficient way to evaluate
erf(x) is to use the truncated power series (this is
easily derived from the integral (1) by expanding the integral as
a power series and integrating term by term. Note that we have
changed x^2 -> 2 x^2 in going from (1) to (2) below):
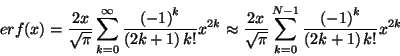 |
(2) |
Equation 2 is a so called alternating power series and
is theoretically convergent for all x. If one truncates the
series at some high order term N-1, the error
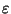 that is made is smaller than the first discarded term.
If x is significantly larger than 1 (5 or larger) then the series in
2 will converge very slowly. Other series expansions (asymptotic
series) can be used in that case. You need not worry about this. If
that is made is smaller than the first discarded term.
If x is significantly larger than 1 (5 or larger) then the series in
2 will converge very slowly. Other series expansions (asymptotic
series) can be used in that case. You need not worry about this. If
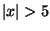 ,
assume that
,
assume that
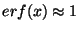 and return this value
without calculating the sum!
and return this value
without calculating the sum!
Phil Duxbury
2000-09-11
![]() to check your answers, because it has this function built in.
to check your answers, because it has this function built in.