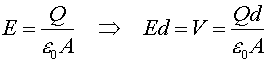
Capacitance of two parallel plates
The most common capacitor consists of two parallel plates. First, we derive the capacitance which depends on the area of the plates A and their separation d. According to Gauss's law, the electric field between two plates is:
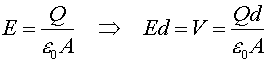
Since the
capacitance is defined by 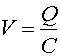 one can see that
capacitance is:
one can see that
capacitance is:
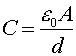
Thus you get the most capacitance when the plates are large and close together. A large capacitance means that the capacitor stores a large amount of charge.
If a dielectric material is inserted between the plates, the microscopic dipole moments of the material will shield the charges on the plates and alter the relation. Materials have a permeability e which is given by the relative permeability k, e=ke0. The capacitance is thus given by:
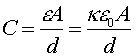
 All materials
have a relative permeability, k, greater than unity, so the capacitance
can be increased by inserting a dielectric. Sometimes, k is
referred to as the dielectric constant of the material. The
electric field causes some fraction of the dipoles in the
material to orient themselves along the E-field as opposed to the
usual random orientation. This, effectively, appears as if
negative charge is lined up against the positive plate, and
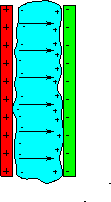
positve charge against the negative plate. In the figure to the
right, the blue material is the dielectric.
All materials
have a relative permeability, k, greater than unity, so the capacitance
can be increased by inserting a dielectric. Sometimes, k is
referred to as the dielectric constant of the material. The
electric field causes some fraction of the dipoles in the
material to orient themselves along the E-field as opposed to the
usual random orientation. This, effectively, appears as if
negative charge is lined up against the positive plate, and
positve charge against the negative plate. In the figure to the
right, the blue material is the dielectric.