Diffuse scattering: Thermal disorder I

Diffuse scattering
Thermal I
Thermal II
Occupational I
Occupational II
Longitudinal waves
Transversal waves
Short range order
Stacking faults
Interactive examples
Displacement waves
Short range order
Stacking faults
Goto
Contents
The first example shows the effect of thermal disorder. The crystal consists of square molecules in a primitive cubic lattice. The each atom is displaced independently at random. The direction of displacement is isotropic, the amplitude of the displacement is Gaussian distributed according to the thermal parameter. The left image shows a part of the crystal, 30*30 unit cells were used for the calculation. The right image shows one quadrant of reciprocal space.

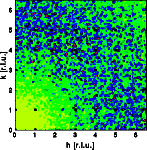
The Bragg reflections are shown as black dots, most of them are overexposed. Diffuse scattering results that is essentially monotonous in reciprocal space. Note that the diffuse scattering is more intense at larger reciprocal vectors h and absent near the origin of reciprocal space a typical phenomenon of displacement disorder.
The Fourier transform of a disordered crystal can be calculated to a first approximation as:
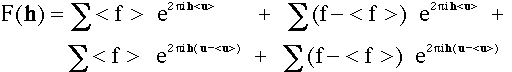
If we consider a structure with a single atom type all terms (f - < f >) are zero. The third term contributes to the diffuse scattering. Its contribution increases, if the phase shift h ( u - < u > ) is large. Near the origin of reciprocal space |h| is small and thus very little phase changes are introduced. As a result the diffuse intensity near the origin is weak. If the displacement of u is non-random as in the case of displacement waves, a non-uniform phase results throughout reciprocal space and thus systematic extinctions of the diffuse scattering / satellites. More about that at the examples about waves.