Interactive guide to diffraction ..

Interactive Tutorial about Diffraction
Diffuse scattering: Thermal disorder II

Diffuse scattering
Thermal I
Thermal II
Occupational I
Occupational II
Longitudinal waves
Transversal waves
Short range order
Stacking faults

Interactive examples
Displacement waves
Short range order
Stacking faults

Goto
Contents

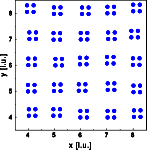
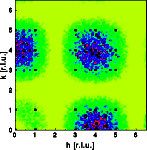
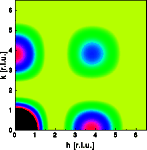
The second example modifies the effect of thermal disorder. Now the crystal consists of rigid square molecules in a primitive cubic lattice. The center of each molecule is displaced at random while the bond lengths and the orientation of the molecule are kept constant. The direction of displacement is isotropic, the amplitude of the displacement is Gaussian distributed according to the thermal parameter. The left image shows a part of the crystal, 30*30 unit cells were used for the calculation. The middle image shows one quadrant of reciprocal space.

The Bragg reflections are shown as black dots, most of them are overexposed. Diffuse scattering results that is modulated in reciprocal space since the atoms are no longer moved independently. Note that the diffuse scattering is more intense at larger reciprocal vectors h and absent near the origin of reciprocal space. The modulation of the diffuse scattering can be explained by calculating the Fourier transform of a single rigid square molecule (right image above). This Fourier transform shows the same modulation as that of the diffuse scattering observed from the disordered crystal. In real space thermally disordered points are convoluted with the molecule. In real space the monotonous Laue scattering is multiplied by the Fourier transform of a single molecule. Since the monotonous Laue scattering is zero at the origin of reciprocal space, the diffuse scattering of this crystal is zero at the origin of reciprocal space as well.