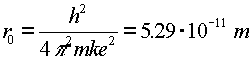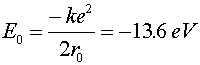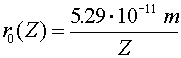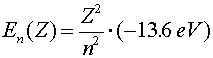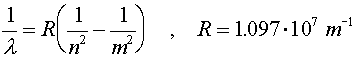The Hydrogen atom Hydrogen is the simplest atom (one proton and one electron), but is still an extremely rich topic for study. The wave-function aspect of quantum mechanics prevents the electron from collapsing into an infinitesimally small orbit with an infinite negative energy. In classical physics, an attractive ~1/r potential could have arbitrarily small orbitals with arbitrarily large binding energies. In quantum physics, the lowest energy orbital is called the ground state. Solving the Schroedinger equation for an electron in an attractive Coulomb potential provides the ground state properties of the hydrogen atom. Ground state properties of hydrogen
Just to be confusing, the subscript 0 which refers to the ground state refers to n = 1, not n = 0.The radius of an electron in the ground state of hydrogen is called the Bohr radius, named after Niels Bohr, a famous Danish physicists. He found the radius by asking the question, "What circular orbit would have a momentum such that the circumference of the orbit would be exactly one DeBroglie wavelength?" To see the derivation, follow this link. When electrons make a jump from one energy level (a specific value of n) to another energy level, a photon is emitted which carries away the necessary energy to satisfy energy conservation. The inverse wavelength (which is proportional to the energy) of the light is then propotional to the change in energy:
R is known as Rydberg's constant. As an exercise, students can solve for R in terms of fundamental constants. The beginning level is denoted by m and the final level is denoted by n. For n = 1, the various wavelengths (m = 2,3,4...) are known as the Lyman series. The Balmer series is the series where n = 2 and the Paschen series is for n = 3. The values of the wavelengths are often called spectral lines because of the lines that appear in diffraction experiments. For a hot hydrogen source, where the atoms are excited thermally and then deexcite via the emission of photons, the Balmer series is in the visible range. |