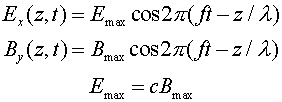|
Maxwell's equations and light
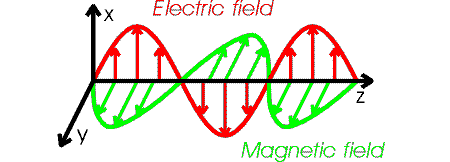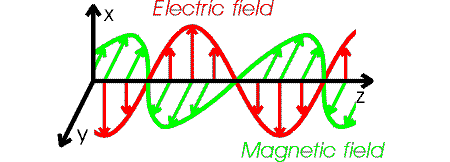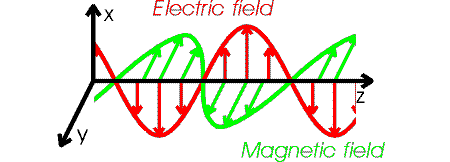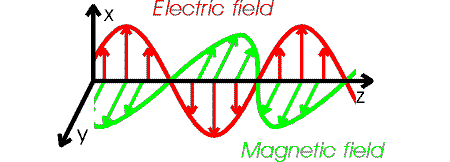
After a bit of non-trivial differential calculus one can show that both the electric and magnetic field obey wave equations. The speed c of an electromagnetic wave is given by: c2 =1/(e0m0) = 2.998 m/s. The details of an electromagnetic wave are fairly complicated. If the wave moves in z-direction, the electric field oscillates in the plane perpendicular to the z-axis. The magnetic field also oscillates and is perpendicular to both the magnetic and electric fields. If the electric field is oscillating in the x-direction, we say the wave is polarized along the x-axis. The figure below illustrates the behavior of an electromagnetic wave which is polarized along the x-axis.
The forms of the electric and magnetic field in the wave are:
where the frequency and wavelength are related by c = fl.. |
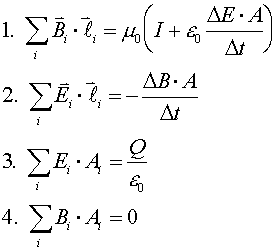Light is
an electromagnetic wave. To explain this, we consider the
Maxwell's equations, the four equations the describe all
of electricity and magnetism. The first equation is
Ampere's law, only that the second term on the
right-hand-side is new. The second equation is Lenz's
law. The third equation is Gauss's law and expresses the
fact that electric field lines begin and end only at
charges. The fourth equation is the magnetic equivalent
of Gauss's law, expressing tha fact that magnetic field
lines never begin or end.
