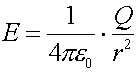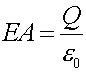Derivation of Gauss's law Gauss's law is another form of Coulomb's law that allows one to calculate the electric field of several simple configurations. Gauss's law relates the electric field lines that "leave" the a surface that surrounds a charge Q to the charge Q inside the surface. Let us compare Gauss's law on the right to Coulomb's law: {note that k has been replaced by 1/(4pe0), where e0 = 1/(4pk) = 8.85E-12}
Here, A refers to the area of a spherical surface that surrounds the charge, which is 4pr2. Gauss's law is more general than Coulomb's law and works whenever the electric field lines are perpendicular to the surface, and Q is the net charge inside the closed surface. If part of the surface is not perpendicular to the closed surface, a cosq term must be added which goes to zero when field lines are parallel to the surface. The adjective "closed" means that the surface must not have any holes. The quantity EA is known as the electric flux, as it can be associated with the net electric field lines that leave the surface. |