Electric fields for simple geometries

Gauss's law can derive the E-field for the following geometries:

1. A spherically symmetric charge distribution, e.g. a point charge.
   The Gaussian surface should be a sphere. The area of the surface is 4pr², so Gauss's law becomes:
   

   
   where Q(r) is the charge inside the surface. For a point charge, Q(r) is the total charge, whereas for a uniform charge density r (charge per unit volume) the charge inside the surface is:
   

   
   

   
   Thus for a uniform sphere of charge, the electric field is zero at r=0, and grows linearly in r inside the sphere, while outside the sphere the electric field is of the same form as Coulomb's law.

2. A large plate with uniform charge density.
   Consider the plate below, which we will assume is infininte ( a good assumption if you are close to the plate) and has a charge per unit area, s.        
                
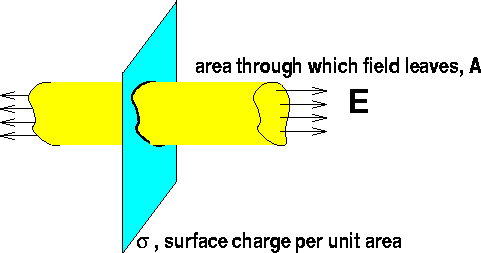
   Gauss's law states (remember the field leaves through both sides):
   

3. Two oppositely charged parallel plates.
   If there were two plates with opposite charge, the electric field would be double this value in between the plates, 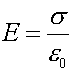,and zero outside the plates.

4. An infinite line charge.
   Drawing a cylinder of length L around an infinite wire, which has a charge per unit length of l, will trap a charge inside of Q=lL, and the area through which the flux leaves is 2prL. Gauss's law then states:
   

Examples     Gauss's law index