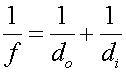Virtual images For an object far away from a concave lens, an image appears at the focal length. As the image is moved closer, the image appears further away. However, when the object reaches the focal length the image moves to infinity, and disappears altogether if the object is within the focal length. When an object is closer than the focal length of a concave mirror, the mirror can no longer reconverge the light. One can see this algebraically by considering the formula
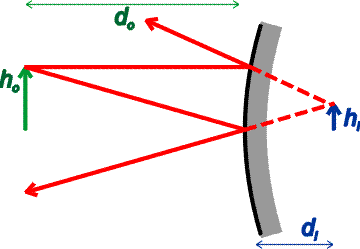
If do is less than f, the image distance di will be negative. This does not mean that there is no image, it merely means that the image appears virtual. That is to say, the light appears as if it comes from behind the mirror. Looking into a mirror in the morning, one sees a virtual image of one's self. In fact, a plane mirror acts like a curved mirror with f set to infinity. In that case di is negative. Convex mirrors never focus light back into a point, but instead always give virtual images as well. In fact for convex mirrors, the focal length is negative, and the same formula applies as above. Let's illustrate a virtual image from a convex mirror.
Many automobile mirrors are convex to cover more angle than a plane mirror. In such mirrors, there is often a warning, Objects may be closer than they appear. |