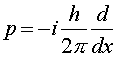The probablilistic interpretation of quantum mechanics A simple question arises about wave functions for particles in quantum mechanics: What is waving? The interpretation is that the wave function Y(x,t) is related to the probability of observing the particle at a given position. The square of the wave function Y equals the probability density P(x,t) of finding the particle at x. Thus in quantum mechanics, one always solves an equation for Y, then one squares Y to find a physically meaningful quantity like a probability. In fact, wave functions are often complex numbers. The equation one solves to find Y is Schroedinger's equation named after the physicist Erwin Schroedinger, who was one of the founders of quantum mechanics in the 1920s. Schroedinger's equation is a differential equation which when written in one dimension is:
Schroedinger's equation looks like energy conservation with the twist that the momentum is replaced by a derivative with respect to the position x. As this equation involves two derivatives, calculus can quickly show that if the potential V is zero that the solution is a simple sine or cosine wave. However, when potentials are added, especially in three dimensions, the math required to solve the equation becomes quite difficult. The solution of this equation for a Coulomb potential yields the quantum properties of atoms which are the subject of the next lecture. |





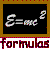


 where
where