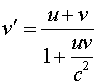Adding velocities Consider two objects. The first object moves with velocity v relative to the second object, while the second object moves with velocity u with respect to an observer. In Newtonian physics the observer would say that the velocity of the first object is the sum of the two velocities.
However, this would allow the observed velocity to exceed the speed of light. In fact, when relativistic effects are accounted for the expression becomes
One can check that this velocity never exceeds the speed of light by working out the result when either u or v equals the speed of light. In that case, v' will be the speed of light. This is consistent with the postulate that the speed of light is the same in all reference frames. Velocity addition problems, can be stated in many ways, often with subtraction of velocities being used rather than addition. The best strategy for approaching some problems is to always write the Newtonian expression first. Then use the relativistic expression above, assigning u and v to whatever velocities are on the right hand side of the expression. If the Newtonian expression has a negative velocity, one must remember to make the velcity in the numerator negative as well. |