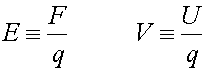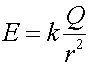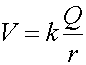Definitions of electric fields and potentials From Physics 231, and from the previous lecture one should be comfortable with the concepts of force and potential energy. From Physics 231, one used the equation:
where Since all electric forces, and therefore potentials are proportional to the charge of an object, it makes sense to define the electric field and electric potential, which are the electric force and the electric potential energy of an object divided by the charge of that object.
Note that the electric potential is NOT THE SAME as electric potential energy. The electric field is a vector(has a direction) and the electric potential is a scalar(has no direction). If one made analagous definitions for for gravity, one would define the gravitational field as the force divided by the mass as the field, and g would be thought of as the gravitational field. If one took the gravitational potential energy mgh(for a constant field) and divided it by the the mass, one would get gh, which would not depend on the mass, and would look like the elevation times g. You can imagine a topographic map as displaying such a quantity. Instead of displaying the energy it takes to lift an object to a certain height, it displays something proportional to the energy, mainly the elevation. For a point charge, the electric field and potential become:
which are one power lower in charge than the force and potential energy defined via Coulomb's law. |