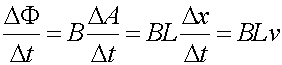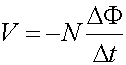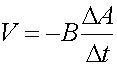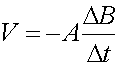Lenz's law We now define the magnetic flux F as a function of the area of a loop and the magnetic field:
We now consider a loop of area A is a constant magnetic field as shown in the previous page concerning motional EMFs. The rate of change of the flux is due to the changing area A.
The area which equals Lx, where x is the position of the bar at some time, changes as Lv. We can then take the expression for the voltage above and write it in terms of the rate change of the flux. The last term is indeed the voltage around the loop derived in the previous page.
This is the equation for induction, Lenz's law. A factor of N was added in case there are multiple loops. We point out that the flux only refers to the B-field lines that pass through the loop. If the field is not oriented perpendicular to the loop there is an additional cosq dependence. The above is more general than the expression for the voltage from the sliding bar above because it demonstrates that one obtains an induced voltage for either
The negative sign has been added to show that if a current was generated from the induced voltage, it would generate a magnetic field in the opposite direction as the change in the flux. |