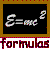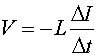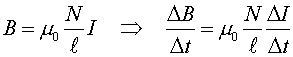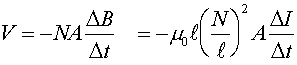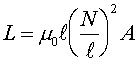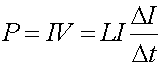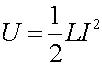Inductance The Inductance L is a measure of the voltage drop across an iductor (e.g. a solenoid) per the rate change of current.
Since the magnetic field inside a solenoid is proportional to a current, the rate-change of the magnetic flux is proportional to the rate-change of the current. From a previous lecture, the magnetic field inside a solenoid was given as:
The voltage across the solenoid is given by the rate-change of the flux times the number of loops:
Therefore, the inductance L can be given in terms of the geometry of the solenoid.
Longer solenoids and solenoids with more cross-sectional area have more inductance. The strongest dependence is on the number of turns per unit length. One can also increase the inductance by using iron instead of a vacuum. One would replace the parameter m0 with m if the material had a different susceptiblity. We have now considered three circuit elements (aside from batteries). The voltage across each element depends on a different aspect of the charge.
A resistor keeps the charge from changing instantly in a circuit, because an instant change in the charge constitutes an infinite current which implies an infinite voltage. Similarly, an inductor keeps the current from changing suddenly. Unlike a capacitor, current can continuously flow through an inductor. An inductor can also store energy. The power being stored in an inductor is:
A little calculus would show that the energy stored in an inductor is:
|