





|

Kirchoff's
laws
There are two
laws necessary for solving circuit problems. For simple
circuits,we have been applying these equations almost
instinctively.
The
voltages around a closed path in a circuit must
sum to zero. (Kirchoff's law #1)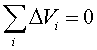 , the voltage
drops being negative (following a current through
a resistor), while the gains are positive (going
through a battery from the negative to the
positive terminal). , the voltage
drops being negative (following a current through
a resistor), while the gains are positive (going
through a battery from the negative to the
positive terminal).
The
sum of the currents entering a node must equal
the sum of the currents exiting a node. (Kirchoff's
Law #2)
The first law is a simple statement
of the meaning of potential. Since every point on a
circuit has a unique value of the potential, travelling
around the circuit, through any path must bring you back
to the potential. Using the analogy to elevation: If one
hikes from a starting point of a mountain, taking several
paths, then finishes at the same point, the sum of the
elevation changes of each path had better add to zero.
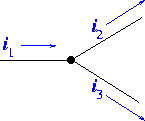 The second law is
the statment of current conservation mentioned before in the
Ohm's law lecture. For the node on the right, i1=i2+i3.
If all currents had been defined as enterning the
node, then the sum of the currents would be zero. The second law is
the statment of current conservation mentioned before in the
Ohm's law lecture. For the node on the right, i1=i2+i3.
If all currents had been defined as enterning the
node, then the sum of the currents would be zero. |
Examples Kirchoff's
laws / RC Circuit's index
|