





|

RC
Circuits
An RC circuit
is simply a circuit with both a resistor and a capacitor.
This combination is useful to study because capacitors
can be used to store energy and a resistor placed along
with the capacitor can control the rate at which energy
is released from the capacitor.
We will
confine our studies to the following type of RC circuit.
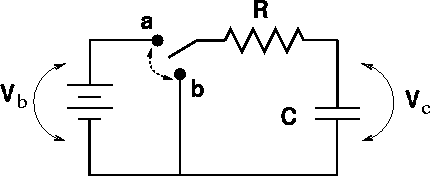
A switch can
be moved from position a to
position b. Before we go
further, let us review some facts about capacitors:
The
charge across a capacitor can not change
instantaneously. Since the change in
charge DQ = IDt, there
must always be a non-zero time before the charge
can change a non-zero amount, unless there were
an infinite current.
There
is no current across a capacitor in steady state.
Since charge builds up on capacitor instead of
flowing through it, current can build up until
the point that the voltage V=Q/C
will balance out the external voltage pushing
charge onto the capacitor.
When a capacitor of capacitance C
is in series with a battery of voltage Vb
and a resistor of resistance R,
the voltage drops must be:
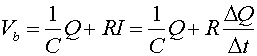 , ,
which is a statement
that the voltage gained going across the battery must
equal the voltage drop across the capacitor plus the
voltage drop across the resistor. An equation where the
rate of change of a quantitity (DQ/Dt)
is proportional to the quantity (DQ) will always
have an exponential solution. We consider two instances:
Discharging
the capacitor: The capacitor initially
is connected (switch in position a)
for a long time, and is then disconnected by
moving the switch to b
at time t = 0. The
capacitor then discharges, leaving the capacitor
without charge or voltage after a long time.
Charging
the capacitor: The switch is in position
b for a long time, allowing the
capacitor to have no charge. At time t
= 0, the switch is changed to a
and the capacitor charges.
| |
Discharging |
Charging |
| Charge |
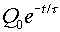 |
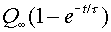 |
| Current |
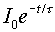 |
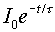 |
| Voltage |
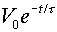 |
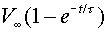 |
Here, Q0,
V0
and I0 refer to the charge, voltage and current of
the capacitor in the instant after the switch is thrown.
The time t is the characteristic time of the decay,
t = RC. When
confronted with an RC problem, the best
strategy is the following:
Decide what
the charge across the capacitor was just before
the switch was thrown. Since the charge can not
change instantly, this is the charge just after
the switch is thrown.
Decide what
the charge is long after the switch is thrown.
Pick the
exponential form for the charge Q(t)
to satisfy the correct initial and final
charges.
The voltage
across the capacitor can be found through, V
= Q/C. The voltages across the
other elements can be found with the help of Kirchoff's
first law.
The current
through a capacitor must always decay and end up
at zero, since charge can not contiuously flow
through a capacitor. The initial current can
usually be ascertained with the help of Ohm's
law, V=RI.
The characteristic time t
= RC tells one that the
charging/discharging is slower with a larger resistor or
capacitor. This makes sense, because a larger resistor
impedes the flow of current; thus slowing the
charging/discharging, and a larger capacitor holds more
charge; thus requiring more time to charge.
Everyone should have a good feeling
for exponential functions. Below are sketches of the
charge Q(t) for the charging
and discharging capacitors.
ajglkajla
Examples Kirchoff's
laws / RC Circuit's index
|








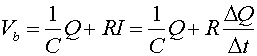 ,
,